Least Mean Squares (LMS) Algorithm#

Author : Payam Parvazmanesh
Contact : payam.manesh@gmail.com
Pattern Recognition
1. Online Algorithms: Definition and Concept#
An online algorithm is a type of algorithm that processes input data in a sequential manner, typically one piece at a time, and updates its model or parameters after each new data point. Unlike offline algorithms, which require all data to be available before any processing begins, online algorithms are well-suited for real-time applications, where data arrives incrementally, such as in streaming data, real-time prediction, or adaptive filtering.
In an online learning process, the model is updated continuously, without the need to reprocess all past data, making it computationally efficient and suitable for dynamic environments.
2. Least Mean Squares (LMS) Algorithm#
The Least Mean Squares (LMS) algorithm is a popular adaptive filtering and optimization algorithm used for solving regression and prediction problems. It is part of the family of online algorithms, meaning it processes data incrementally, updating the model parameters after each new data point. The main goal of the LMS algorithm is to minimize the prediction error by adjusting the model weights iteratively.
Problem Setup#
In a typical regression scenario, we have a set of input-output pairs. The inputs are represented as vectors \(( x_k )\), and the corresponding desired outputs are represented by scalars \(( y_k )\). We are interested in finding a set of model parameters \(( w )\) that predict the output as accurately as possible. The predicted output is given by:
where:
\(( x_k )\) is the input vector for the \(( k )-th\) sample,
\(( w )\) is the parameter vector (weights),
\(( \hat{y}_k )\) is the predicted output for the \(( k )-th\) sample.
The error for the \(( k )-th\) sample is defined as the difference between the desired output \(( y_k )\) and the predicted output \(( \hat{y}_k )\):
The goal is to update the weights \(( w )\) in such a way that the error \(( e_k )\) is minimized over time.
Loss Function#
The loss function used in the LMS algorithm is typically the Sum of Squared Errors (SSE). For a single data point, the squared error is:
To simplify the optimization process, we use a scaled version of this loss function:
Where:
\(( J(w) )\) is the cost function (which is the sum of squared errors),
\(( \frac{1}{2} )\) is included to simplify the calculation of gradients.
This cost function measures the discrepancy between the predicted output \(( w^T x_k )\) and the desired output \(( y_k )\).
Gradient Descent: Weight Update Rule#
The LMS algorithm uses gradient descent to minimize the cost function. The gradient of the cost function with respect to the weights \(( w )\) is calculated as:
This gradient points in the direction of the steepest increase in the cost function. To minimize the cost function, we update the weights in the opposite direction of the gradient. The weight update rule becomes:
Where:
\(( w_k )\) is the weight vector at the \(( k )-th\) iteration,
\(( \mu )\) is the learning rate, a positive constant that determines the step size for the weight update,
\(( x_k )\) is the input vector at the \(( k )-th\) iteration,
\(( y_k )\) is the desired output for the \(( k )-th\) sample.
Online Learning: Adaptive Update Rule#
Since LMS is an online algorithm, the weight update occurs after each individual data sample. This means the algorithm adapts and updates the weights incrementally as new data points arrive, without requiring all data to be available beforehand. The update rule for the LMS algorithm is:
Where:
\(( w_k )\) is the weight vector at iteration \(( k )\),
\(( \mu )\) is the learning rate,
\(( y_k )\) is the desired output at iteration \(( k )\),
\(( x_k )\) is the input feature vector at iteration \(( k )\),
\(( w_k^T x_k )\) is the predicted output.
This equation shows that the weight vector is adjusted based on the error \(( e_k = y_k - w_k^T x_k )\) and the input vector \(( x_k )\).
LMS Algorithm with Correntropy Loss#
The Least Mean Squares (LMS) algorithm is widely used in adaptive filtering and regression problems, where the goal is to iteratively adjust model parameters to minimize the error between the predicted output and the desired output. In its basic form, the LMS algorithm minimizes the squared error loss. However, in certain applications, particularly in situations involving noisy data or non-Gaussian noise, a more robust loss function can be used to enhance the performance of the LMS algorithm. One such alternative is the correntropy loss, which offers greater robustness against outliers and non-Gaussian noise by emphasizing more on higher-order moments.
Correntropy Loss#
Correntropy measures the similarity between two variables by emphasizing not only their average (mean) differences but also higher-order statistical relationships. It is particularly effective in environments where noise is non-Gaussian or data contains outliers.
The correntropy loss function is defined as:
where:
\(( e_k = y_k - w^T x_k )\): The error between the desired output \(( y_k )\) and the model prediction \(( w^T x_k )\) at iteration \(( k )\),
\(( \sigma )\): A parameter that controls the sensitivity of the loss function to the magnitude of errors.
Unlike the squared error loss, this formulation downweights the impact of large errors, making it more robust to outliers.
LMS Algorithm with Correntropy Loss#
To adapt the LMS algorithm to minimize correntropy loss, the weight update process follows the gradient descent method. The cost function for a single data point is:
Gradient of the Correntropy Cost Function#
The gradient of \(( J(w) )\) with respect to the weight vector \(( w )\) is:
Step 1: Take the Derivative of the Loss Function#
The goal is to compute the gradient of the loss \(( J(w) )\) with respect to the weight vector \(( w )\). The derivative of \(( J(w) )\) is computed using the chain rule.
We start by differentiating the exponential term:
Step 2: Differentiate the Exponential Function#
First, apply the chain rule to differentiate the exponential term:
Step 3: Differentiate the Inner Term#
Now, we compute the derivative of the term inside the exponential, which is \(( - \frac{(y_k - w^T x_k)^2}{2 \sigma^2} )\). This can be differentiated as follows:
This is derived by applying the chain rule to the squared term \(( (y_k - w^T x_k)^2 )\), which gives \(( -2(y_k - w^T x_k) x_k )\), and then dividing by \(( 2 \sigma^2 )\).
Step 4: Combine the Terms#
Now, substitute this derivative back into the expression for \(( \nabla_w J(w) )\):
Step 5: Final Gradient Expression#
Thus, the gradient of the correntropy loss with respect to \(( w )\) is:
where:
\(( (y_k - w^T x_k) )\): The error signal,
\(( \exp\left(-\frac{(y_k - w^T x_k)^2}{2 \sigma^2}\right) )\): A weighting function that reduces the influence of large errors.
Weight Update Rule#
Using gradient descent, the weights are updated iteratively to minimize the loss:
where \(( \mu )\) is the learning rate.
Substituting the gradient of \(( J(w) )\), the update rule becomes:
Advantages of LMS with Correntropy Loss#
Robustness to Outliers: The exponential weighting in the loss function reduces the impact of large errors, improving the algorithm’s stability in the presence of outliers.
Non-Gaussian Noise Handling: This loss function is well-suited for environments with non-Gaussian noise, achieving more reliable parameter updates compared to squared error loss.
Higher-order Statistical Adaptation: Unlike squared error loss, the correntropy loss incorporates information about higher-order statistics, enabling more nuanced error handling.
import numpy as np
import matplotlib.pyplot as plt
# Generate some sample data for testing
np.random.seed(0)
N = 100 # Number of samples
X = np.linspace(0, 10, N) # Input data
true_weights = 2.5 # True weight for generating output
noise = np.random.normal(0, 1, N) # Gaussian noise
Y = true_weights * X + noise # Desired output with noise
# Initialize parameters
w = 0 # Initial weight (model parameter)
mu = 0.01 # Learning rate
epochs = 5 # Number of epochs for training
# Arrays to store weights and error values for analysis
weights = []
errors = []
# LMS Algorithm
for epoch in range(epochs):
for i in range(N):
# Compute prediction
y_pred = w * X[i]
# Calculate error
error = Y[i] - y_pred
# Update weight using LMS rule
w = w + 2 * mu * error * X[i]
# Store weight and error
weights.append(w)
errors.append(error)
# Plotting results
plt.figure(figsize=(12, 5))
# Plot the error over iterations
plt.subplot(1, 2, 1)
plt.plot(errors, color='blue')
plt.xlabel('Iteration')
plt.ylabel('Error')
plt.title('Error over Iterations')
# Plot the learned model versus true relationship
plt.subplot(1, 2, 2)
plt.scatter(X, Y, label='Data')
plt.plot(X, w * X, color='red', label='LMS Learned Model')
plt.plot(X, true_weights * X, color='green', linestyle='--', label='True Model')
plt.xlabel('Input X')
plt.ylabel('Output Y')
plt.legend()
plt.title('LMS Learned Model vs. True Model')
plt.tight_layout()
plt.show()
print("Final learned weight:", w)
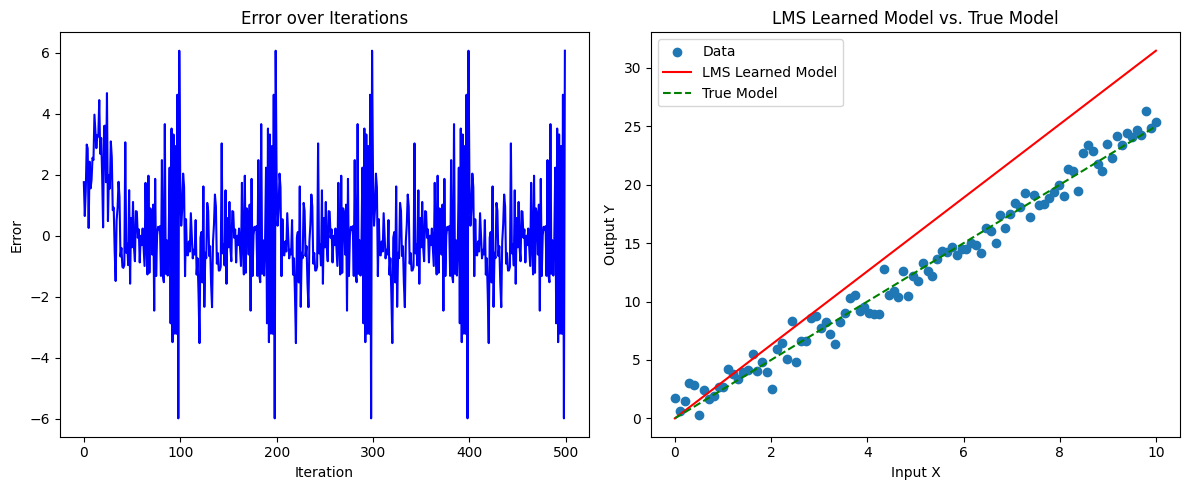
Final learned weight: 3.147543439836432
Kernel Least Mean Squares (KLMS) Algorithm#
The Kernel Least Mean Squares (KLMS) algorithm is an extension of the traditional Least Mean Squares (LMS) algorithm, designed to handle nonlinear problems by using kernel methods. The core idea behind KLMS is to apply a nonlinear transformation (via a kernel function) that maps the input data into a higher-dimensional feature space. This allows the KLMS to approximate nonlinear relationships, something the standard LMS cannot do. Below, we will derive the key formulas for KLMS, step by step, explaining how we arrive at each equation and why these steps are taken.
Step 1: Prediction with Kernel Function#
In the traditional LMS algorithm, the predicted output \(( \hat{y}_n )\) at time step \(( n )\) is computed as a weighted sum of the input features:
Where \(( \mathbf{w} )\) is the weight vector and \(( \mathbf{x}_n )\) is the input vector at time step \(( n )\).
However, in KLMS, we use kernel functions to map the input vector \(( \mathbf{x}_n )\) into a higher-dimensional feature space. Instead of computing a simple dot product, we use a kernel function \(( k(\mathbf{x}_i, \mathbf{x}_n) )\) that computes the similarity between the input vector \(( \mathbf{x}_n )\) and all previous input vectors \(( \mathbf{x}_i )\). This allows us to approximate nonlinear functions.
Thus, the predicted output \(( \hat{y}_n )\) in KLMS is:
Where:
\(( \hat{y}_n )\) is the predicted output at time step \(( n )\),
\(( \alpha_i )\) are the weight coefficients corresponding to the input vectors \(( \mathbf{x}_i )\),
\(( k(\mathbf{x}_i, \mathbf{x}_n) )\) is the kernel function that computes the similarity between \(( \mathbf{x}_i )\) and \(( \mathbf{x}_n )\).
Why Use Kernels?#
The kernel function allows us to implicitly map the input vectors into a higher-dimensional feature space, without explicitly computing the mapping. This transformation makes it possible for KLMS to approximate complex, nonlinear relationships between inputs and outputs, which standard LMS cannot.
Step 2: Compute the Prediction Error#
The prediction error \(( e_n )\) at time step \(( n )\) is defined as the difference between the desired output \(( d_n )\) and the predicted output \(( \hat{y}_n )\):
Where:
\(( e_n )\) is the error at time step \(( n )\),
\(( d_n )\) is the desired output at time step \(( n )\),
\(( \hat{y}_n )\) is the predicted output at time step \(( n )\).
This error term \(( e_n )\) represents how far the model’s prediction is from the true value.
Step 3: Update the Weights#
The goal of KLMS, like LMS, is to adjust the weights so as to minimize the prediction error. We do this by applying an update rule based on the gradient of the cost function. For KLMS, the cost function is typically the Mean Squared Error (MSE):
To minimize the cost function \(( J(\alpha) )\), we perform gradient descent. The gradient of the cost function with respect to the weight coefficients \(( \alpha )\) is:
We now need to compute the derivative of \(( \hat{y}_n )\) with respect to the coefficients \(( \alpha_i )\). Using the kernel-based prediction equation:
Taking the derivative with respect to \(( \alpha_i )\) gives:
Thus, the gradient of the cost function with respect to \(( \alpha_i )\) becomes:
The update rule for the weight coefficients \(( \alpha_i )\) at time step \(( n )\) is then:
Where:
\(( \alpha_{n+1} )\) is the updated weight coefficient at time step \(( n )\),
\(( \alpha_n )\) is the current weight coefficient at time step \(( n )\),
\(( \eta )\) is the learning rate (a constant that controls the step size of the update),
\(( k(\mathbf{x}_n, \mathbf{x}_n) )\) is the kernel function evaluated at the current input \(( \mathbf{x}_n )\).
Why This Update Rule?#
This weight update rule ensures that the weights \(( \alpha_n )\) are adjusted in the direction that reduces the error \(( e_n )\), thus improving the accuracy of the model’s predictions. The kernel function \(( k(\mathbf{x}_n, \mathbf{x}_n) )\) measures the similarity between the current input and itself, and this is used to scale the weight update.
Step 4: Kernel Function Selection#
The kernel function \(( k(\mathbf{x}_i, \mathbf{x}_j) )\) plays a crucial role in the performance of KLMS. Some commonly used kernel functions include:
Gaussian (Radial Basis Function) Kernel: $\( k(\mathbf{x}_i, \mathbf{x}_j) = \exp \left(-\frac{\|\mathbf{x}_i - \mathbf{x}_j\|^2}{2\sigma^2}\right) \)$ This kernel is popular for its ability to map inputs into an infinite-dimensional space, which makes it suitable for complex, highly nonlinear relationships.
Polynomial Kernel: $\( k(\mathbf{x}_i, \mathbf{x}_j) = (\mathbf{x}_i^\top \mathbf{x}_j + c)^d \)$ Where:
\(( c )\) is a constant,
\(( d )\) is the degree of the polynomial. This kernel is useful for capturing interactions between features when they can be represented by polynomial relationships.
Summary of KLMS Algorithm#
The KLMS algorithm is an adaptive filtering technique that uses kernel methods to model nonlinear relationships. The key steps of the algorithm are:
Compute the predicted output} using the kernel function: $\( \hat{y}_n = \sum_{i=1}^{n} \alpha_i \cdot k(\mathbf{x}_i, \mathbf{x}_n) \)$
Compute the prediction error: $\( e_n = d_n - \hat{y}_n \)$
Update the weight coefficients based on the error: $\( \alpha_{n+1} = \alpha_n + \eta \cdot e_n \cdot k(\mathbf{x}_n, \mathbf{x}_n) \)$
import numpy as np
import matplotlib.pyplot as plt
# Generate some sample nonlinear data for testing
np.random.seed(0)
N = 100 # Number of samples
X = np.linspace(-5, 5, N) # Input data
true_weights = 0.5 # This will only affect the output to simulate a pattern
noise = np.random.normal(0, 1, N) # Gaussian noise
Y = np.sin(X) + true_weights * X + noise * 0.1 # Desired output with noise
# KLMS Parameters
mu = 0.1 # Learning rate
sigma = 1.0 # Kernel width for Gaussian kernel
epsilon = 0.1 # Threshold for adding new dictionary elements
# Initialize dictionary and coefficients
dictionary = []
coefficients = []
# Gaussian kernel function
def gaussian_kernel(x, c, sigma):
return np.exp(-np.linalg.norm(x - c)**2 / (2 * sigma**2))
# Kernel Least Mean Squares (KLMS) algorithm
for i in range(N):
x_i = X[i]
y_i = Y[i]
# Predict output using dictionary elements
y_pred = 0
for j, c in enumerate(dictionary):
y_pred += coefficients[j] * gaussian_kernel(x_i, c, sigma)
# Compute error
error = y_i - y_pred
# If the error exceeds epsilon, add the new input to the dictionary
if abs(error) > epsilon:
dictionary.append(x_i)
coefficients.append(mu * error)
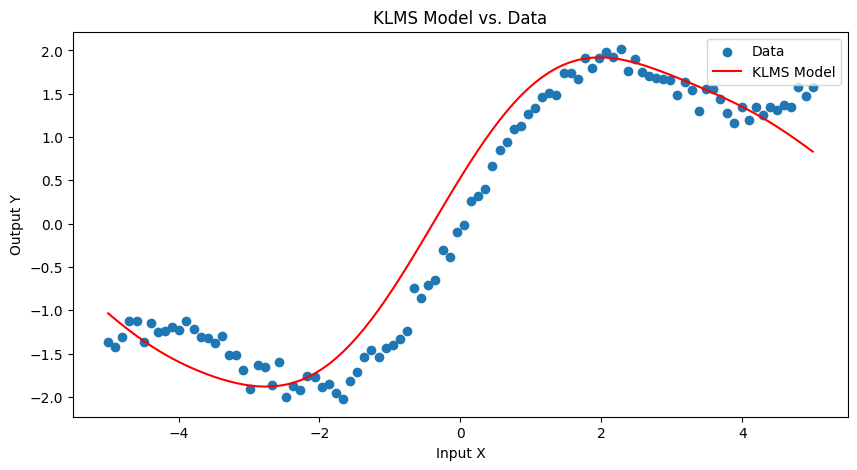
# Plotting the results
plt.figure(figsize=(10, 5))
# Plot original data and KLMS predictions
plt.scatter(X, Y, label='Data')
plt.plot(X, [sum(coeff * gaussian_kernel(x, c, sigma) for coeff, c in zip(coefficients, dictionary)) for x in X], color='red', label='KLMS Model')
plt.xlabel('Input X')
plt.ylabel('Output Y')
plt.legend()
plt.title('KLMS Model vs. Data')
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics.pairwise import rbf_kernel
from sklearn.decomposition import PCA
def generate_data(num_samples=10, num_features=3):
"""
Generate synthetic 3D data with a non-linear target function.
"""
np.random.seed(0)
X = np.random.rand(num_samples, num_features)
y = np.sin(np.sum(X, axis=1)) # Non-linear target
return X, y
def apply_rbf_kernel(X, sigma=0.5):
"""
Apply the RBF kernel to the input data and return the kernel matrix.
"""
return rbf_kernel(X, X, gamma=1 / (2 * sigma ** 2))
def klms_algorithm(X, y, kernel_matrix, learning_rate=0.1, iterations=50):
"""
Perform Kernel Least Mean Squares (KLMS) algorithm.
"""
alpha = np.zeros(X.shape[0]) # Initialize coefficients (weights)
errors = []
for n in range(iterations):
for i in range(X.shape[0]):
# Compute the predicted output for the current input
predicted = np.sum(alpha * kernel_matrix[i, :]) # Kernel-weighted sum
# Compute the error
error = y[i] - predicted
errors.append(error)
# Update the alpha coefficients
alpha += learning_rate * error * kernel_matrix[i, :]
return alpha, errors
def plot_error_curve(errors):
"""
Plot the error curve during KLMS learning.
"""
plt.figure(figsize=(8, 5))
plt.plot(errors)
plt.title("KLMS Error Curve")
plt.xlabel("Iteration")
plt.ylabel("Error")
plt.show()
def main():
# Generate data
X, y = generate_data(num_samples=10, num_features=3)
# Visualize the original data
visualize_data(X, y, title="Original 3D Data")
# Apply RBF Kernel
sigma = 0.5
K = apply_rbf_kernel(X, sigma)
# Perform KLMS
learning_rate = 0.1
iterations = 50
alpha, errors = klms_algorithm(X, y, K, learning_rate, iterations)
# Reduce the kernel matrix to 2D using PCA for visualization
pca = PCA(n_components=2)
X_pca = pca.fit_transform(K) # Perform PCA on the kernel matrix
# Plot the error curve
plot_error_curve(errors)
# Show final alpha coefficients
print("Final alpha coefficients after KLMS:")
print(alpha)
if __name__ == "__main__":
main()
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[3], line 85
80 print(alpha)
84 if __name__ == "__main__":
---> 85 main()
Cell In[3], line 60, in main()
57 X, y = generate_data(num_samples=10, num_features=3)
59 # Visualize the original data
---> 60 visualize_data(X, y, title="Original 3D Data")
62 # Apply RBF Kernel
63 sigma = 0.5
NameError: name 'visualize_data' is not defined
