Covariance

• Author : Poorya Fekri

• Contact : Poorya_fekri@gmail.com

fundamental & definition:

We will talk about the covariance of two random variables, which gives us useful information about the dependencies between these two random variables. It’s analagous to how we define variance, except now we have an X and a Y. cause we’re looking at joint distributions. $\( \text{cov}(X, Y) = \mathbb{E}\left[ (X - \mathbb{E}[X]) \cdot (Y - \mathbb{E}[Y]) \right] \)\( first of all, it's a product of something times something. So we've brought the \)X\( (relative to its mean) and the \)Y\( (relative to its mean) together into one thing, cause we're trying to see how they vary together. The analog of that formula which is a generalization is: \)\( \text{cov}(X, Y) = \mathbb{E}[(X - \mathbb{E}[X])(Y - \mathbb{E}[Y])] \\\)\( \)\(=\mathbb{E}[XY - X\mathbb{E}[Y] - \mathbb{E}[X]Y + \mathbb{E}[X]\mathbb{E}[Y]] \\ \)\( \)\(= \mathbb{E}[XY] - \mathbb{E}[X]\mathbb{E}[Y] - \mathbb{E}[X]\mathbb{E}[Y] + \mathbb{E}[X]\mathbb{E}[Y] \\ \)\( \)\(= \mathbb{E}[XY] - \mathbb{E}[X]\mathbb{E}[Y] \)$

Examle:

Imagine we have five samples each of apples and pears, and we want to examine their characteristics. Naturally, they have many features, but for simplicity, we’ll focus on just two. The first feature is the size of the fruits, represented by integers. The second is the proportion of the upper half to the lower half, expressed as a float and referred to as “shape.”.

\[\begin{split} \text{Apples} =X = \begin{bmatrix} 3 & 2 & 3 & 4 & 5 \\ 1 & 0.9 & 1 & 0.8 & 0.9 \end{bmatrix} \end{split}\]

\[\begin{split} \text{Pears} =Y = \begin{bmatrix} 3 & 4 & 4 & 6 & 7 \\ .7 & 0.6 & .6 & 0.4 & 0.3 \end{bmatrix} \end{split}\]

To understand how the size of pears changes in relation to their proportion, we need to calculate the covariance between these two features for pears. If we define the fruit dataset to include both apples and pears, we can then analyze the relationship between the size of the fruits and their proportions by applying the covariance equation to the entire dataset.

1. Covariance for pears between their size and shape :

Steps to Calculate Covariance:

Let’s define pear’s size as \( Y_1 \) (First row of the matrix Y) and pear’s shape as \( Y_2 \) (Second row of the matrix Y) so:

• \( Y_1 = [3, 4, 4, 6, 7] \)

• \( Y_2 = [0.7, 0.6, 0.6, 0.4, 0.3] \)

Steps to Calculate Covariance

1. Calculate the Means of our features:

   \[ \bar{Y_1} = \frac{3 + 4 + 4 + 6 + 7}{5} = \frac{24}{5} = 4.8 \]
   \[ \bar{Y_2} = \frac{0.7 + 0.6 + 0.6 + 0.4 + 0.3}{5} = \frac{2.6}{5} = 0.52 \]

2. Calculate Deviations from the Mean:

   \[ Y_1' = [3 - 4.8, 4 - 4.8, 4 - 4.8, 6 - 4.8, 7 - 4.8] = [-1.8, -0.8, -0.8, 1.2, 2.2] \]
   \[ Y_2' = [0.7 - 0.52, 0.6 - 0.52, 0.6 - 0.52, 0.4 - 0.52, 0.3 - 0.52] = [0.18, 0.08, 0.08, -0.12, -0.22] \]

3. Calculate the Products of Deviations:

   \[ Y_1 \cdot Y_2 = [-1.8 \times 0.18, -0.8 \times 0.08, -0.8 \times 0.08, 1.2 \times -0.12, 2.2 \times -0.22] = [-0.324, -0.064, -0.064, -0.144, -0.484] \]

4. Sum the Products:

   \[ \sum Y_1 \cdot Y_2 = -0.324 - 0.064 - 0.064 - 0.144 - 0.484 = -1.08 \]

5. Calculate the Covariance: The covariance is given by:

\[ \text{Cov}(Y_1, Y_2) = \frac{\sum (Y_{1i}' \times Y_{2i}')}{n - 1} = \frac{-1.08}{5 - 1} = \frac{-1.08}{4} = -0.27 \]

The covariance is \( -0.27 \), indicating a negative relationship between the variables. As we gather more samples, this estimate will likely become more accurate, offering a clearer understanding of the strength and direction of the relationship. .

In the next step, we can combine these datasets to explore how the features of all fruits vary together. By examining both the shape and size of all fruits collectively, we can better understand how these features relate to each other

2. Covariance for Fruit data set :

\(X = \begin{bmatrix} 3 & 2 & 3 & 4 & 5 \\ 1 & 0.9 & 1 & 0.8 & 0.9 \end{bmatrix}\)

\(Y = \begin{bmatrix} 3 & 4 & 4 & 6 & 7 \\ 0.7 & 0.6 & 0.6 & 0.4 & 0.3 \end{bmatrix}\)

Combine the datasets \(X\) and \(Y\)

We horizontally concatenate the two datasets to form:

\(\text{Combined} = \text{C} =\ \begin{bmatrix} 3 & 2 & 3 & 4 & 5 & 3 & 4 & 4 & 6 & 7 \\ 1 & 0.9 & 1 & 0.8 & 0.9 & 0.7 & 0.6 & 0.6 & 0.4 & 0.3 \end{bmatrix}\)

Calculate the covariance:

1. Calculate the mean

\[ \text{First Row} = \bar{C_1} = \frac{3 + 2 + 3 + 4 + 5 + 3 + 4 + 4 + 6 + 7}{10} = 4.1\]

\[ \text{Second Row} = \bar{C_2} = \frac{1 + 0.9 + 1 + 0.8 + 0.9 + 0.7 + 0.6 + 0.6 + 0.4 + 0.3}{10} = 0.72\]

2. Compute deviations from the mean

For the size : $\((3 - 4.1), (2 - 4.1), (3 - 4.1), (4 - 4.1), (5 - 4.1), (3 - 4.1), (4 - 4.1), (4 - 4.1), (6 - 4.1), (7 - 4.1)\)$

For the shape: $\((1 - 0.72), (0.9 - 0.72), (1 - 0.72), (0.8 - 0.72), (0.9 - 0.72), (0.7 - 0.72), (0.6 - 0.72), (0.6 - 0.72), (0.4 - 0.72), (0.3 - 0.72)\)$

3. Finally

\[ \text{Cov}(X_1, X_2) = \frac{\sum (X_{1i}' \times X_{2i}')}{n - 1} = \frac{-2.62}{10 - 1} = \frac{-2.62}{6} = -0.291 \]

some properties:

To prove every property of the covariance we can simply use the difinition. The covariance between two random variables \( X \) and \( Y \) is defined as:

\[ \operatorname{cov}(X, Y) = \mathbb{E}[(X - \mathbb{E}[X])(Y - \mathbb{E}[Y])] \]

Where \( \mathbb{E}[X] \) and \( \mathbb{E}[Y] \) are the expected values (means) of \( X \) and \( Y \), respectively, so:

\( \begin{aligned} (1).\operatorname{cov}(X, a) & =0 \\ \end{aligned} \)

In our case, let \( Y = a \), where \( a \) is a constant.

\[ \mathbb{E}[a] = a \]

\[ \operatorname{cov}(X, a) = \mathbb{E}[(X - \mathbb{E}[X])(a - \mathbb{E}[a])] \]

\[ \operatorname{cov}(X, a) = \mathbb{E}[(X - \mathbb{E}[X])(a - a)] = \mathbb{E}[(X - \mathbb{E}[X])(0)] \]

\[ \operatorname{cov}(X, a) = \mathbb{E}[0] = 0 \]

\( \begin{aligned} (2).\operatorname{cov}(X, X) & =\operatorname{var}(X) \\ \end{aligned}\) For \(Y\) \(=\) \(X\) :

\[ \operatorname{cov}(X, X) = \mathbb{E}[(X - \mathbb{E}[X])(X - \mathbb{E}[X])] \]

\[ \operatorname{cov}(X, X) = \mathbb{E}[(X - \mathbb{E}[X])^2] \]

\[ \operatorname{var}(X) = \mathbb{E}[(X - \mathbb{E}[X])^2] \]

\[ \operatorname{cov}(X, X) = \operatorname{var}(X) \]

\( \begin{aligned} (3).\operatorname{cov}(X, Y) & =\operatorname{cov}(Y, X) \\ \end{aligned}\)

\[ \operatorname{cov}(X, Y) = \mathbb{E}[(X - \mathbb{E}[X])(Y - \mathbb{E}[Y])] \]

\[ \operatorname{cov}(Y, X) = \mathbb{E}[(Y - \mathbb{E}[Y])(X - \mathbb{E}[X])] \]

\[ \operatorname{cov}(X, Y) = \mathbb{E}[(X - \mathbb{E}[X])(Y - \mathbb{E}[Y])] = \mathbb{E}[(Y - \mathbb{E}[Y])(X - \mathbb{E}[X])] \]

\[ \operatorname{cov}(X, Y) = \operatorname{cov}(Y, X) \]

\( \begin{aligned} (4).\operatorname{cov}(a X, b Y) & =a b \operatorname{cov}(X, Y) \\ \end{aligned}\)

\[ \operatorname{cov}(a X, b Y) = \mathbb{E}[(a X - \mathbb{E}[a X])(b Y - \mathbb{E}[b Y])] \]

\[ \mathbb{E}[a X] = a \mathbb{E}[X] \quad \text{and} \quad \mathbb{E}[b Y] = b \mathbb{E}[Y] \]

\[ \operatorname{cov}(a X, b Y) = \mathbb{E}[(a X - a \mathbb{E}[X])(b Y - b \mathbb{E}[Y])] \]

\[ = \mathbb{E}[(a (X - \mathbb{E}[X]))(b (Y - \mathbb{E}[Y]))] = ab \mathbb{E}[(X - \mathbb{E}[X])(Y - \mathbb{E}[Y])] \]

\[ \operatorname{cov}(a X, b Y) = a b \operatorname{cov}(X, Y) \]

\( \begin{aligned} (5).\operatorname{cov}(X+a, Y+b) & =\operatorname{cov}(X, Y) \\ \end{aligned}\)

\[ \operatorname{cov}(X + a, Y + b) = \mathbb{E}[(X + a - \mathbb{E}[X + a])(Y + b - \mathbb{E}[Y + b])] \]

\[ \mathbb{E}[X + a] = \mathbb{E}[X] + a \quad \text{and} \quad \mathbb{E}[Y + b] = \mathbb{E}[Y] + b \]

\[ (X + a - \mathbb{E}[X + a]) = (X - \mathbb{E}[X]) \quad \text{and} \quad (Y + b - \mathbb{E}[Y + b]) = (Y - \mathbb{E}[Y]) \]

\[ \operatorname{cov}(X + a, Y + b) = \mathbb{E}[(X - \mathbb{E}[X])(Y - \mathbb{E}[Y])] \]

\[ \operatorname{cov}(X + a, Y + b) = \operatorname{cov}(X, Y) \]

\( \begin{aligned} (6).\operatorname{cov}(a X+b Y, c W+d V) & =a c \operatorname{cov}(X, W)+a d \operatorname{cov}(X, V)+b c \operatorname{cov}(Y, W)+b d \operatorname{cov}(Y, V) \\ \end{aligned}\)

\[ \operatorname{cov}(a X + b Y, c W + d V) = \mathbb{E}[(a X + b Y - \mathbb{E}[a X + b Y])(c W + d V - \mathbb{E}[c W + d V])] \]

\[ \mathbb{E}[a X + b Y] = a \mathbb{E}[X] + b \mathbb{E}[Y] \quad \text{and} \quad \mathbb{E}[c W + d V] = c \mathbb{E}[W] + d \mathbb{E}[V] \]

\[ (a X + b Y - \mathbb{E}[a X + b Y]) = a(X - \mathbb{E}[X]) + b(Y - \mathbb{E}[Y]) \]

Useful fact: From the \(2^{\text{nd}}\) and \(6^{\text{th}}\) property it can be concluded that: $\( \text{var}(X_1 + X_2) = \text{var}(X_1) + \text{var}(X_2) + 2 \cdot \text{cov}(X_1, X_2) \)$ So if these two variables’ covariance is zero, the variance of their sum is equel to sum of their varience.

Finally, it must be noted that the covariance between two random variables \(X\) and \(Y\) is zero when there is no linear relationship between them. However, zero covariance does not necessarily imply independence; it only indicates that the variables are uncorrelated.

Proof

Let \( X \) be a, random variable uniformly distributed on the interval [-1, 1], and let \(Y\) \(=\) \(X^2\).

1. \( \mathbb{E}[X] \): $\( \mathbb{E}[X] = \int_{-1}^{1} x \cdot f_X(x) \, dx = \int_{-1}^{1} x \cdot \frac{1}{2} \, dx \)\( \)\( \mathbb{E}[X] = \frac{1}{2} \int_{-1}^{1} x \, dx \)\( \)\( \int_{-1}^{1} x \, dx = \left. \frac{x^2}{2} \right|_{-1}^{1} = \frac{1^2}{2} - \frac{(-1)^2}{2} = 0 \)\( \)\( \mathbb{E}[X] = \frac{1}{2} \times 0 = 0 \)$

2. \( \mathbb{E}[Y] = \mathbb{E}[X^2] \): $\( \mathbb{E}[X^2] = \int_{-1}^{1} x^2 \cdot \frac{1}{2} \, dx \)\( \)\( \mathbb{E}[X^2] = \frac{1}{2} \int_{-1}^{1} x^2 \, dx \)\( \)\( \int_{-1}^{1} x^2 \, dx = \left. \frac{x^3}{3} \right|_{-1}^{1} = \frac{1^3}{3} - \frac{(-1)^3}{3} = \frac{2}{3} \)\( \)\( \mathbb{E}[X^2] = \frac{1}{2} \times \frac{2}{3} = \frac{1}{3} \)$

3. \( \operatorname{cov}(X, Y) \): $\( \operatorname{cov}(X, Y) = \mathbb{E}[X \cdot Y] - \mathbb{E}[X] \cdot \mathbb{E}[Y] = \mathbb{E}[X \cdot Y] = \mathbb{E}[X \cdot X^2] = \mathbb{E}[X^3] \)\( \)\( \mathbb{E}[X^3] = \int_{-1}^{1} x^3 \cdot \frac{1}{2} \, dx \)\( \)\( \mathbb{E}[X^3] = \frac{1}{2} \int_{-1}^{1} x^3 \, dx \)\( \)\( \int_{-1}^{1} x^3 \, dx = \left. \frac{x^4}{4} \right|_{-1}^{1} = \frac{1}{4} - \frac{1}{4} = 0 \)\( \)\( \mathbb{E}[X^3] = \frac{1}{2} \times 0 = 0 \)$

\( \operatorname{cov}(X, Y) = 0 \),indicating no linear relationship between \(X\) and \(Y\). However, since \(Y\) \(=\) \(X^2\),it is dependent on \(X\).Therefore, \(X\) and \(Y\) are not independent despite having zero covariance.

Examle:

covariance calculation of independant and dependant sample values to illustrate the correlation between covariance and dependancy.

import numpy as np
import matplotlib.pyplot as plt

# Set a random seed
np.random.seed(42)
mean=[0,0]
cov_matrix_X_Y=[[1,0],[0,1]]
cov_matrix_normal=[[1,1],[1,1]]
# Generate random samples
n_samples = 1000


# Generate dependent variables X and Y
data = np.random.multivariate_normal(mean, cov_matrix_X_Y, n_samples)
X = data[:,0]
Y = data[:,1]
# Calculate covariance between independent X and Y
covariance_XY = np.mean(X * Y) - np.mean(X) * np.mean(Y)
print(f"Covariance between X and Y that are independent: {covariance_XY}")



# Generate dependent variables X and Y normal
data2 = np.random.multivariate_normal(mean, cov_matrix_normal, n_samples)
X_normal = data2[:,0]
Y_normal = data2[:,1]
# Calculate covariance between X and Y dependent to eachother
covariance_XY_normal = np.mean(X_normal * Y_normal) - np.mean(X_normal) * np.mean(Y_normal)
print(f"Covariance between X and Y that are dependent: {covariance_XY_normal}")



# Generate dependent variables Z and W which are deoendent with zero covariance
Z = X  # Z is just X
W = X**2  # W is non-linearly related to X
# Calculate covariance between Z and W
covariance_ZW = np.mean(Z * W) - np.mean(Z) * np.mean(W)
print(f"Covariance between Z=X and W=X^2 that are defined dependently but have zero covariance: {covariance_ZW}")

Covariance between X and Y that are independent: 0.0025195790600571998
Covariance between X and Y that are dependent: 1.0154178285599225
Covariance between Z=X and W=X^2 that are defined dependently but have zero covariance: 0.041494076988932704

Covariance Matrix

The covariance matrix generalizes the concept of covariance to multiple dimensions (random variables). For \( d \) random variables, the covariance matrix \( C \) is a \( d \times d \) matrix where each element \( C_{i,j} \) represents the covariance between the \( i \)-th and \( j \)-th random variables:

\[ C_{i,j} = \sigma(x_i, x_j) \]

Properties of the covariance matrix:

• Dimension: \( C \in \mathbb{R}^{d \times d} \), where \( d \) is the number of random variables.

• Symmetry: The covariance matrix is symmetric since \( \sigma(x_i, x_j) = \sigma(x_j, x_i) \).

• Diagonal Entries: The diagonal entries are the variances of the individual random variables.

• Off-Diagonal Entries: The off-diagonal entries are the covariances between different random variables.

The covariance matrix \( C \) for \( n \) samples and \( d \) dimensions can be calculated as:

\[ C = \frac{1}{n-1} \sum^{n}_{i=1} (x_i - \bar{x})(x_i - \bar{x})^T \]

where:

• \( x_i \) is the \( i \)-th sample vector (a \( d \)-dimensional vector).

• \( \bar{x} \) is the mean vector of the samples, defined as \( \bar{x} = \frac{1}{N} \sum^{N}_{i=1} x_i \).

\[\begin{split} \quad C = \begin{bmatrix} x_1^{(1)} & x_2^{(1)} & \ldots & x_d^{(1)} \\ x_1^{(2)} & x_2^{(2)} & \ldots & x_d^{(2)} \\ \vdots & \vdots & \ddots & \vdots \\ x_1^{(N)} & x_2^{(N)} & \ldots & x_d^{(N)} \end{bmatrix} \end{split}\]

For a two-dimensional example with variables \( x \) and \( y \), the covariance matrix \( C \) can be written as:

\[\begin{split} C = \left( \begin{array}{cc} \sigma(x, x) & \sigma(x, y) \\ \sigma(y, x) & \sigma(y, y) \end{array} \right) \end{split}\]

If \( x \) and \( y \) are independent (or uncorrelated), the covariance matrix simplifies to:

\[\begin{split} C = \left( \begin{array}{cc} \sigma_x^2 & 0 \\ 0 & C_y^2 \end{array} \right) \end{split}\]

For standardized variables (with mean 0 and variance 1), the covariance matrix would approximate:

\[\begin{split} C = \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right) \end{split}\]

This matrix indicates that the variables are uncorrelated and have unit variance.

Example:

Remember our last example for five apples and pears.

Now we once calculate the covariance but this time in the cov-matrix format:

\[\begin{split} \text{Fruits} = \begin{bmatrix} 3 & 2 & 3 & 4 & 5 & 3 & 4 & 4 & 6 & 7 \\ 1 & 0.9 & 1 & 0.8 & 0.9 & 0.7 & 0.6 & 0.6 & 0.4 & 0.3 \end{bmatrix} \end{split}\]

Step 1: Calculate the Covariance Matrix

Covariance between two random variables \( X \) and \( Y \) is calculated using the formula:

\[ \text{Cov}(X, Y) = \frac{1}{n - 1} \sum_{i=1}^{n} (X_i - \bar{X})(Y_i - \bar{Y}) \]

where:

• \( n \) is the number of data points,

• \( X_i \) and \( Y_i \) are the individual elements of the datasets,

• \( \bar{X} \) and \( \bar{Y} \) are the mean values of the datasets.

For a dataset with \(N\) variables, the covariance matrix \( C \) is calculated as:

\[ C = \frac{1}{n - 1} (A - \bar{A}) (A - \bar{A})^T \]

where:

• \( A \) is the dataset matrix (our combined dataset),

• \( \bar{A} \) is the mean of each row in \( A \),

• \( A - \bar{A} \) is the deviation from the mean,

• The resulting matrix \( C \) is the covariance matrix.

Step 2: Apply to the Dataset

Form the covariance matrix by applying the covariance formula to the deviations:

The covariance matrix is:

\[\begin{split} C = \begin{bmatrix} 2.322 & -0.291 \\ -0.291 & 0.060 \end{bmatrix} \end{split}\]

Step 3: Interpret the Covariance Matrix

• \( C_{11} = 2.322 \): This is the variance of the first variable (first row of the combined dataset).

• \( C_{22} = 0.060 \): This is the variance of the second variable (second row of the combined dataset).

• \( C_{12} = C_{21} = -0.291 \): This is the covariance between the two variables, indicating a slight negative linear relationship between them.

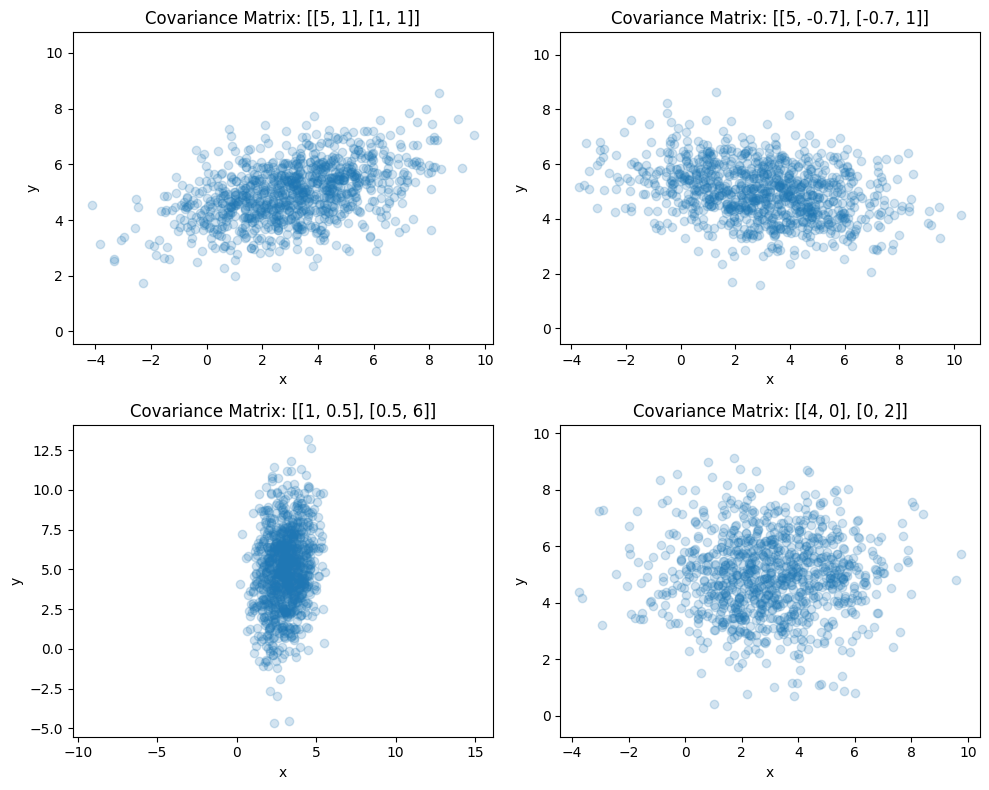
Example: Sampling from the Mean with Different Types of Covariance

You can modify the elements of the covariance matrix defined in the following code:

cov_matrix are = [[5, 1], [1, 1]], 
    [[5, -3], [-3, 1]], 
    [[1, 7], [7, 6]], 
    [[4, 0], [0, 2]]]

import numpy as np
import matplotlib.pyplot as plt

# Number of samples
n = 1000
mean = [3, 5]
# Define the covariance matrices
covariances = [
    [[5, 1], [1, 1]], 
    [[5, -.7], [-.7, 1]], 
    [[1, .5], [.5, 6]], 
    [[4, 0], [0, 2]]]
#figure with subplots
fig, axs = plt.subplots(2, 2, figsize=(10, 8))

for ax, cov_matrix in zip(axs.flat, covariances):
    # Generate samples from the multivariate normal distribution
    data = np.random.multivariate_normal(mean, cov_matrix, n)
    # Split the data into x and y components  
    x = data[:, 0]
    y = data[:, 1]
    # Calculate the mean and covariance of the generated data
    calculated_mean = np.mean(data, axis=0)
    calculated_cov = np.cov(data, rowvar=False)

    # Plot the generated samples
    ax.scatter(x, y, alpha=0.2)
    ax.set_title(f'Covariance Matrix: {cov_matrix}')
    ax.set_xlabel('x')
    ax.set_ylabel('y')
    ax.axis('equal')
    
#layout
plt.tight_layout()
plt.show()

References:

-Statistics 110 (Probability) taught at Harvard University by Joe Blitzstein(Professor of the practice in statistics, Harvard University)-Lecture 21